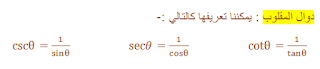نُشر بواسطة : مريهان الزبيدي
السبت، 29 أبريل 2017
الجمعة، 28 أبريل 2017
احتمالات الحوادث المتنافية
احتمالات الحوادث المتنافية
المفردات :
الحادثتنان
المتنافيتان .
الحادثة المتممة.
الحوادث المتنافية :
عند إيجاد احتمال
وقوع حادثة أو وقوع حادثة أخرى , يجب أن تعرف العلاقة بين الحادثتين . فإذا لم يكن
وقوع الحادثتين ممكناً في الوقت نفسه يقال إنهما متنافيتان ؛ أي أنه لا توجد نواتج
مشتركة بينهما .
مثال :
حدد إذا كانت
الحادثتان متنافيتين أم غير متنافيتين في كل مما يأتي وبرر إجابتك :
يمكن لأي طالب في
الصفوف الأول والثاني والثالث الثانوي
الترشح ليكون مسؤول
أنشطة . ويرغب صالح أن يكون المسؤول من الصف الثاني الثانوي أو الثالث الثانوي .
في حين يرغب سلمان في أن يكون السؤول من الصف الأول الثانوي . أو طالباً يبدأ اسمه
بحرف م
المسؤؤل من الصف الثاني
الثانوي أو الثالث الثانوي .
هاتان الحادثتان
متنافيتان ؛ لأنه ليس بينهما نواتج مشتركة , إذ لايمكن أن يكون المسؤول طالباً في
الصف الثالث والثاني في آن واحد .
المسؤول طالب من الصف الأول
الثانوي أو طالب يبدأ اسمه بحرف م .
هاتان حادثتان غير
متنافيتان ؛ لأنه يمكن أن يكون المسؤول من الصف الأول الثانوي وفي الوقت نفسه يبدأ
اسمه بحرف م .
قوانين الاحتمال
إعداد : شريفة بايحيى .
عنوان الدرس : الدوال المثلثيه في المثلثات القائمة الزاوية
حساب
المثلثات : هو العلاقة بين زويا المثلث وأضلاعه
.
النسبة
المثلثيه : هي مقارنة بين طولي ضلعين في
المثلث القائم الزاوية .
*عند
استعمال الدوال المثلثيه يجب ان تكون الزاوية حادة في مثلث قائم الزاوية وإذا لم
تكن كذلك فإن الزاوية تكون غير معرفة .
* لإيجاد معكوس النسب المثلثيه باستعمال
الآلة الحاسبة أقوم بالضغط على SHIFT
ثم
الدالة المثلثيه المراد ايجاد معكوسها
شرح مثال 1
إيجاد قيم الدوال المثلثيه
اذا كانت 𝞠 تمثل
قياس زاوية حادة في المثلث القائم الزاوية فيC , فأوجد قيم الدوال
المثلثيه الست للزاوية 𝞠 عندما
يكون : طول الضلع المقابل للزاوية𝞠 : BC=8 , طول
الضلع المجاور للزاوية 𝞠 :AC +15 ,طول الوتر AB=17
في البداية سنقوم بإيجاد اول ثلاث دوال مثلثيه فعندما
نوجد sin , cos , tan سنستطيع ايجاد csc , sec , cot بسهول فعند ايجاد sin , cos , tan فقط سنقوم
بقلب العدد لتصبح الدالة صحيحة .
شرح
مثال 2 إيجاد
النسب المثلثيه
شرح مثال 3
إيجاد طول ضلع مجهول
شرح
مثال 5 إيجاد قياس
زاوية مجهولة
الخميس، 27 أبريل 2017
الاحتمال والتباديل مع التكرار
الاحتمال والتباديل مع التكرار .
في احد برامج الألعاب يعطى المتسابق احرفا مبعثرة ويطلب إليه تكوين كلمة وفق دلائل محددة :
هناك 7 أحرف يتكرر فيها حرف الألف مرتين والحرف ياء مرتين , ولذا فإن عدد التباديل المختلفه لهذه الأحرف هو :
الاحتمال والتباديل الدائرية .
أمنه محمد
الخميس، 16 مارس 2017
تابع المتسلسلات الحسابية.
مثال 3 ( ايجاد الأوساط الحسابية )
اوجد الاوساط الحسابية في المتتابعة (22,....,....,.....,.....-8)
الخطوة الأولى : بما أنه يوجد 4 حدود بين الحد الأول والحد الأخير فإن حدود المتتابعة هو 4+2=6 إذن n=6
الخطوة الثانية : اوجد قيمة d
an=a1+(n-1)d
22=-8+(6-1)d
30=5d
6=d
استعمل d لايجاد الاوساط الاربعة المطلوبة
22⟷16⟷10⟷4⟷-2⟷-8 كل مرة نزود 6
الاوساط الحسابية هي 2,4,10,16,22-
تحقق من فهمك )
المتسلسلات الحسابية\ هي حدود متتابعة حسابية .
يسمى ناتج جمع الحدود n الأولى من المتسلسلة المجموع الجزئي ويرمز له بالرمز sn
رمز المجموع :
يمكن التعبير عنه باستعمال هذه الصورة المختصرة.
رمز الاجابة الصحيحة هو c
والحمدلله رب العالمين وصلى الله وسلم على سيدنا محمد وعلى اله وصحبه أجمعين.⧭
عنوان الدرس : المتتابعات والمتسلسلات الحسابية
مالفرق بين المتتابعة والمتسلسلة الحسابية ؟
المتتابعة يكون بين حدودها فواصل مثل ( 1،2، 3، 4،)
المتسلسلة يكون بين حدودها اشارة الجمع مثل ( 1+2+3+4)
في المتسلسلات الحسابية سنستعمل هذا القانون :
مثال 1 ايجاد حد معين في متتابعة حسابية
مثال 1
اوجد قيمة الحد الثاني عشر في الممتابعة الحسابية 9,16,23,30,
الخطوة الأولى :أوجد أساس المتتابعة
لايجاد أساس المتتابعة نطرح العدد الثاني من العدد الأول
16-9=7
23-16=7 ونكمل بالطريقة هذي ع جميع الاعداد الباقية
واساس المتتابعة هو7
الخطوة الثانية : اوجد قيمة الحد الثاني عشر
الحد الأول وهو 9 = a1، الأساس وهو 7 = d ، n=12
an=a1+(n-1)d
a12+9(12-1)(7)
9+77=86
تحقق من فهمك
a1)
anعلما بأن : n=9 , d=6 ,a1=-4
المطلوب الحد التاسع للمتابعة
مثال 2
( كتابة صيغة
الحد النوني لمتتابعة حسابية )
تحقق من فهمك
2a)
....,6-,12,3
طريقة الحل
أول شيء نكتب القانون
an=a1+(n-1)d
ثاني شيء نوجد الاساس لانو مو موجود عندنا
نطرح العدد الثاني من العدد الأول (3-12=-9)
d=-9
ونبدا نعوض
an=a1+(n-1)d
9-(an=12+(n-1
9 + 12-9=an
an=-9n+21
الاثنين، 6 مارس 2017
تابع درس: المتتابعات بوصفها دوالّ
تمثيل المتتابعة الهندسية بيانياً:
- في المتتابعةالحسابية : ...18,14,10,
أوجد الحدود الأربعة التالية في هذه المتتابعة.
الشرح:نحسب أساس المتتابعة فمثلاً أساس المتتابعة هنا هو 4-10 = 4- إذا هذا العدد يمثل الفرق المشترك بين حدود المتتابعة.
- للإيجاد الحد التالي يجب إضافة (أجمع ) 4- للحد الأخير المُعطى.
(4-)+ (4- )+ ( 4- )+ (4- )+
إذاً الحدود الأربعة المتتالية للمتتابعة هي: 6 , 2 , 2- , 6-
- مثل الحدود السبعة الأولى من المتتابعة بيانياً.
الحل:
وتمثل بيانياً كما في الشكل:
تصنيف المتتابعات.
إذاً الحدود الأربعة المتتالية للمتتابعة هي: 6 , 2 , 2- , 6-
- مثل الحدود السبعة الأولى من المتتابعة بيانياً.
الحل:
تصنيف المتتابعات.
حدد نوع المتتابعة في كل مما يأتي , هل هي حسابية أم هندسية أم غير ذلك . ووضح إجابتك:
ِ..., 54 , 36 , 24 , 16
أوجد الفرق بين كل حديت متتاليين.
أوجد الفرق بين كل حديت متتاليين.
خطأ
- أوجد النسبة بين كل حدين متتاليين .
- أوجد النسبة بين كل حدين متتاليين .
بما أن النسبة بين كل حدين متتاليين ثابتة فإن المتتابعة هندسية .
نشر بواسطة/ خلود إبراهيم .
بما أن النسبة بين كل حدين متتاليين ثابتة فإن المتتابعة هندسية .
نشر بواسطة/ خلود إبراهيم .
نشر بواسطة/ خلود إبراهيم .
الاشتراك في:
الرسائل
(
Atom
)